[Talk on LLM] – [Talk on RLHF] – [Slides of LLM Talk] – [Tweet Thread of the LLM Talk]
- The presenter Hyungwon Chung is a research engineer at OpenAI; he was with Google. He was doing mechanical engineering during Ph.D. that is completely irrelevant (aka. pressure-retarded osmosis) from machine learning.
- The “Pretraining” section mostly comes from the LLM talk. The other sections are from the RLHF talk.
Pretraining
-
Functional Viewpoint of the Transformer LM
The transformer could be viewed as a computation module that receives and outputs the matrices of size
(b, d, l). All powerful LLMs are based on transformers. The interaction between tokens have minimal assumptions: each token could interact with any other token; this is done using a mechanism called “dot-product attention.”
For the sake of efficiency, the process above is done in batches. The only interdependence across the batch is finally the loss is divided by the batch size
b.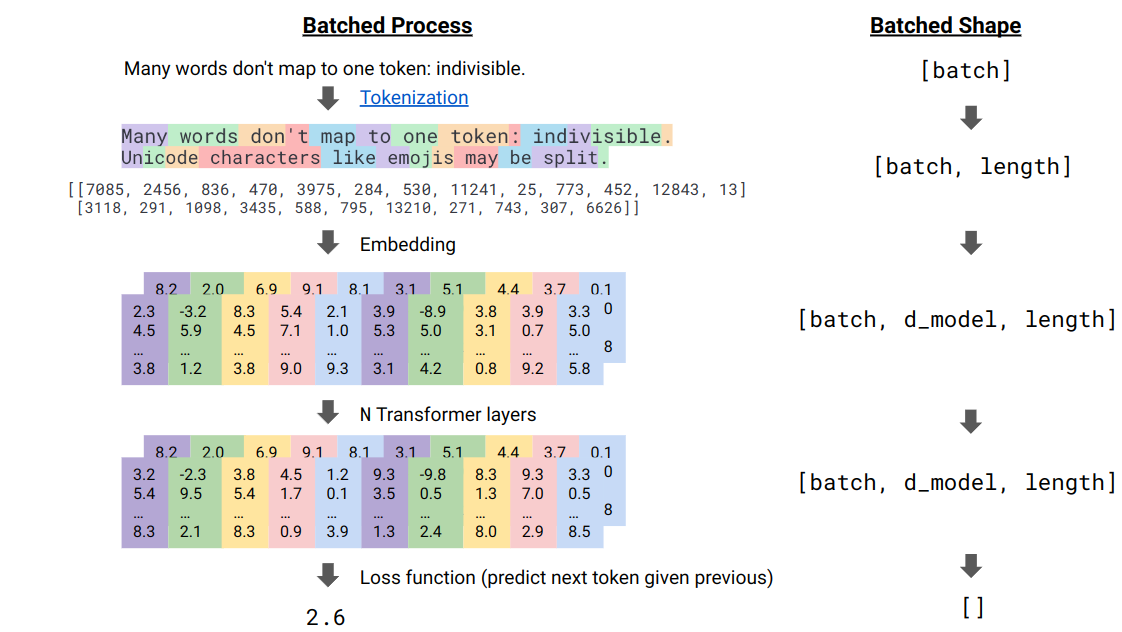
-
Scaling Transformers
This means efficiently doing matrix multiplication with many machines (with matrices distributed on each and every machine) while minimizing the communication costs between machines.
-
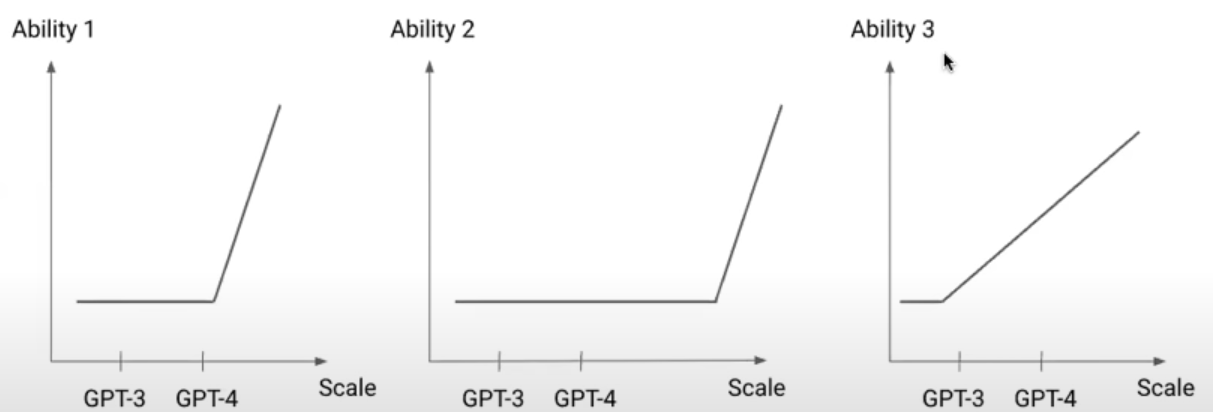
Scaling Law, Phase Change, and Emergent Abilities
- An idea that does not work now may work when scaling up the model size. We need to constantly unlearn intuitions built on outdated or even invalidated ideas. We can update our intuition by reruning experiments that previously do not work on newer models and pinpointing what is new in these newer models.
- Post Training
- Users could not immediately communicate with the pretrained model as the training objective of pretraining is next token prediction. Prompt engineering mitigates this problem by setting up the ground for the LM to generate the relevant content.
- Pretrained models always generate something that is a natural continuation of the prompts even if the content is malicious.
Supervised Fine-Tuning (SFT)
-
Instruction tuning is the technique that will almost universally beneficial to decoder only model and encoder-decoder model to improve their performances: the answer to “should I try instruction tuning” is almost always “yes.”
Importantly, this is true even if we use encoder-only model as instruction-tuning provides a better initialization for “single-task” fine-tuning (see [2]). For example, we could use instruction-tuned BERT rather than regular BERT for various tasks.
Pareto Improvements to Single Task Finetuning For both sets of Held-In and Held-Out tasks examined, finetuning Flan-T5 offers a pareto improvement over finetuning T5 directly. In some instances, usually where finetuning data is limited for a task, Flan-T5 without further finetuning outperforms T5 with task finetuning.
-
An Unified Architecture
All tasks are unified with the single text-to-text format (proposed by T5). This was not obviously a valid choice because back to that time people do not believe LMs could “understand.”
-
Two Flavors of Instruction Tuning
- Using Mixture of Academic Datasets: Flan and T0. The limitation of these models is that they could not generate longer texts due to the limitation of the academic datasets.
- Using User Traffic: For example, InstructGPT and ChatGPT. The user traffics are unavaialble in the academic datasets (for example, “explain the moon landing to a six year old.”) as there is no way to evaluate them.
-
Task Diversity and Model Size are Important
- The T0 by the presenter collects 1836 tasks; it is still the largest collections as of November 2023. The authors show the linear scaling law of model size and normalized performance on the held-out tasks. Further, when the number of tasks increase, the line is lifted upwards with a double digit gain. Further, it is important to have combine the non-CoT and CoT data together.
- However, the performance quickly plateaus even when there are more tasks. This is likely due to limited diversity of academic datastes.
-
Inherent Limitation of Instruction Tuning
For a given input, the target is the single correct answer (it could be called behavior cloning in RL); this requires formalizing correct behavior of a given input. However, this is hard or even impossible for inputs that look like the following:
- Write a letter to a 5-year-old boy from Santa Clause explaining that Santa is not real. Convey gently so as not to break his heart.
- Implement Logistic regression with gradient descent in Python.
The issue is that (1) the correct answer may not be unique, and (2) it is hard or even impossible to provide the correct answer. However, the tension is that none of the existing functions could directly address these issues. The solution is using rewards in RL to address the problem.
RLHF
The lecture is based on the InstructGPT paper, which provides the foundational idea and popularize RLHF. There are many variants and extensions of this papers; they are easy to understand if we understand this foundational paper.
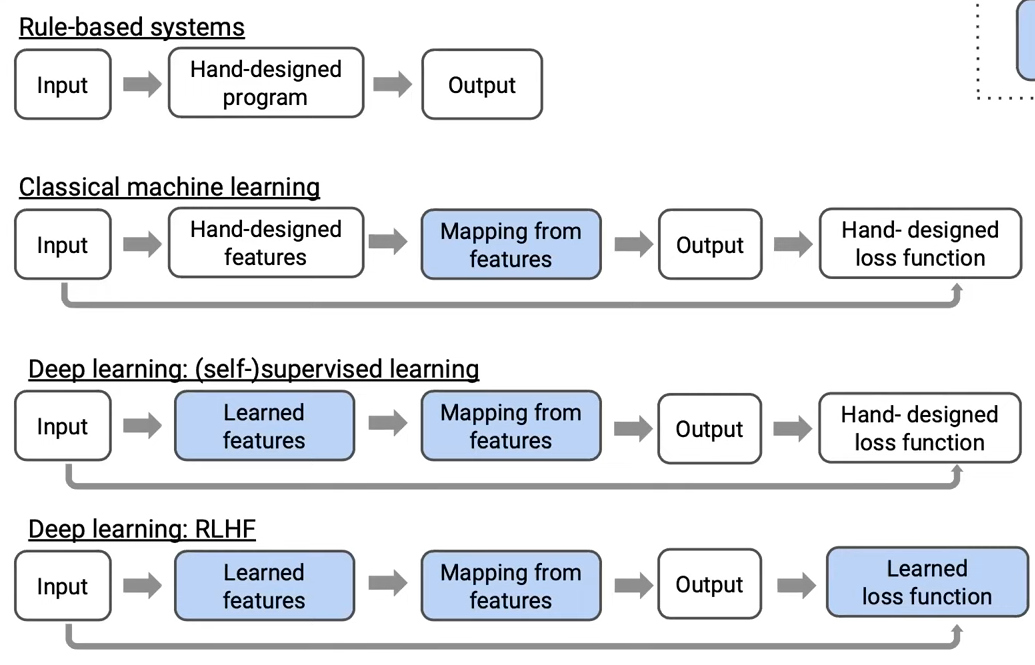
The goal of RLHF is encoding human preferences and (more generally) values. RLHF opens up a new paradigm of learning the objective function; the inductive bias from rule-based system to RLHF is gradually removed for more general use cases (the blue block refers to the learnable block within a system).
Reward Model (RM)
The intuition of training a reward model is It is difficult to evaluate open-ended generation directly, but it is easier to compare two completions.
The reward model r(x, y;\phi) is the SFT model that replaces the last layer with a layer that outputs a scalar; it could also be done differently like taking the probability of [CLS] token, etc. As long as the model outputs a scalar, how exactly we model this process is less relevant.
Let p _ {ij} be the probability that the completion y _ i is better than y _ j (here the order matters), then based on the old Bradley-Terry model; the function r(\cdot) models the strength of the sample. Note that it is likely both y _ i and y _ j are bad, then the goal is to choose the one that is relatively better.
\log \frac{p _ {ij}}{ 1 – p _ {ij}} = r(x, y _ i ; \phi) – r(x, y _ j; \phi),\quad p _ {ij} = \sigma( r(x, y_i;\phi) – r(x, y _ j; \phi))
Then we want to find \phi so that the sum of the probabilities is maximized: \max _ \phi \sum _ {x, y _ i, y _ j \in D} \log p _ {ij}.
Note that there are some issues with the reward modeling; there are many ways to improve this scheme:
- The scheme above does not model how much y _ i is better than y _ j.
Policy Model
Once we have the reward model r(\cdot), we could use that to update the parameters of the language model itself \pi _ \theta. Specifically, we would like to maximize the following. Note that the prompt X=(X _ 1, \cdots, X _ S) are from academic datasets or user traffic and completion Y = (Y _ 1, \cdots, Y _ T) are sampled from the language model \pi _ \theta; the reward model is fixed in this process.
J(\theta) = \mathbb{E} _ {(X, Y)\sim D _ {\pi _ \theta}} \left[ r(X, Y;\phi) \right]
The specific algorithm used to update \theta is PPO as it could give a stable gradient update. Here is the procedure:
- Initialize the policy model to a SFT model.
-
Repeat the following:
- Sampling: Sampling prompts from the input datasets.
- Rollout: Generating the completion conditiong on the prompt with the current LM \pi _ \theta.
-
Evaluation: Computing the reward of the input and the generated output using the (fixed) reward model r(x, y;\phi). Note that the reward model is not necessarily a model according to
trllibrary, it could also come from a rule or a human. - Optimization: Back-propagating the policy model and updating the parameter.
The explanation is alreay clear. To make the understanding more concrete, we could take a look at the MWE provided by trl library.

One issues (asked by He He) is that there might be distribution shift when applying the fixed reward model here; it could be an interesting problem to study: should we perodically update reward model (through something like continual learning) so that the distribution shift is mitigated?
Regularization
-
Preventing \pi _ \theta from Deviating Too Much from the SFT Model (Overfitting to RM or Reward Hacking)
Adding the per-token penalty to prevent \pi _ \theta(Y\vert X) from growing too large compared to \phi _ \text{SFT}(Y\vert X). The intuition why this is important is that RM may model some human bias (for example, preference for longer texts) that may not be ideal for the task to solve.
J(\theta) = \mathbb{E} _ {(X, Y)\sim D _ {\pi _ \theta}} \left[ r(X, Y;\phi) – \beta \log \frac{\pi _ \theta(Y\vert X)}{\pi _ \text{SFT}(Y\vert X)}\right]
Additional Notes
- There is no reliable metrics to measure long generated texts; this is a problem not solved even for OpenAI.
- The inputs are typically longer than outputs. This is one of the reasons why the models trained on the open-source datasets perform poor.
- The easier tasks (for example, simple arithmetic like
3 + 2 =) is already solved pretty well by the pretrained models. The goal of the SFT and RLHF is to address the diverse and abstract prompts. - The RM is called preference model by Anthropic.
- When we have k responses to the same input, we could form \binom{k}{2} sample pairs and put them in the same batch to avoid overfitting.
- The Constitutional AI (CAI) by Anthropic almost automates everything during RLHF; the only human efforts involved is writing the constitution itself. For example, the model is tasked to generate prompts; these prompts are sent to train reward models.
np.einsum()is the extension ofnp.matmul().
Reference
- [2210.11416] Scaling Instruction-Finetuned Language Models (Chung et al., including Jason Wei)
- [2301.13688] The Flan Collection: Designing Data and Methods for Effective Instruction Tuning (Longpre et al.)
- [2009.01325] Learning to summarize from human feedback (Stiennon et al.): An example of reward hacking.
- [2212.08073] Constitutional AI: Harmlessness from AI Feedback (Bai et al.)