[Semantic Scholar] – [Code] – [Tweet] – [Video] – [Website] – [Slide] – [HuggingFace]

Change Logs:

• 2023-09-06: First draft. This paper appears at ICLR ’20.
• 2023-09-07: Add the “example” section for easy visualization.

Background

ERM and DRO

• ERM

  ERM tries to minimize the empirical risk. Here \hat{P} denotes the empirical distribution of the true underlying distribution P of training data.

\hat{\theta} _ \mathrm{ERM} := \mathbb{E} _ {(x, y) \sim \hat{P}} \left[ \ell((x, y); \theta)\right]

• DRO

  DRO tries to find \theta that minimizes the worst-group risk \hat{\mathcal{R}}(\theta). The practical form of DRO is called group DRO (i.e., gDRO). See the application section on how the groups are defined.

\hat{\theta} _ \mathrm{DRO} := \arg\min _ \theta \left[ \hat{\mathcal{R}}(\theta):=\max _ {g \in \mathcal{G}}\mathbb{E} _ {(x, y) \sim \hat{P} _ g} \left[ \ell(x, y); \theta) \right] \right]

Example

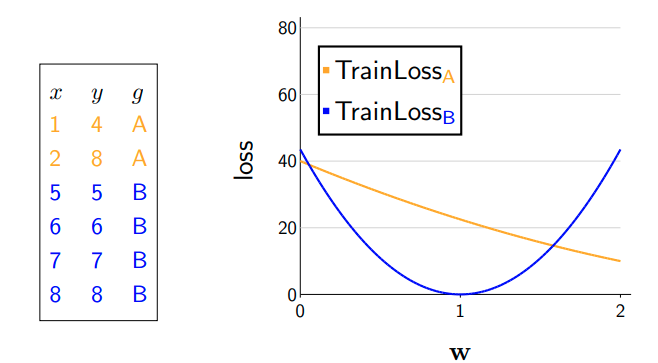
To better visualize the strength of gDRO over ERM, we can look at a linear regression example; this example is taken from Stanford CS 221.

The objective of linear regression is Mean Square Error (MSE) \arg\min_{\mathbf{w}} (\mathbf{w}^T\mathbf{x} -y) ^ 2; fitting the entire datasets gives a much higher group A loss (i.e. 21.26) than group B loss (i.e. 0.31) even though the total loss is 7.29.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

x = np.array([1, 2, 5, 6, 7, 8])[:, np.newaxis]
y = np.array([4, 8, 5, 6, 7, 8])

reg = LinearRegression(fit_intercept=False)
reg.fit(x, y)

print(mean_squared_error(reg.predict(x[:2]), y[:2]))
print(mean_squared_error(reg.predict(x[2:]), y[2:]))
print(mean_squared_error(reg.predict(x), y))

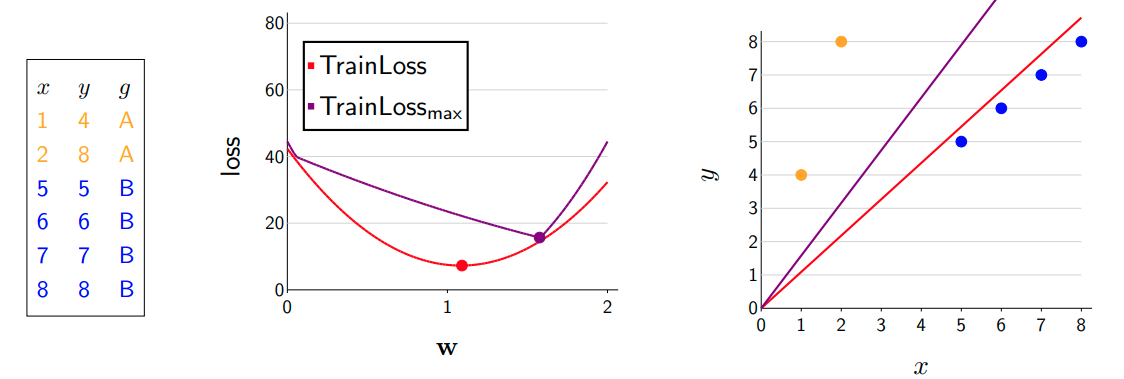
Note that the second plot shows how changing \mathbf{w} leads to differences in the loss over each group (yellow or blue) and the aggregated group (red). We can see that optimizing the aggregated loss leads to a solution that bias group B. However, if we optimize the pointwise maximum (purple), we could improve have a more reasonable curve.

Application

• Mitigating Spurious Correlation

  In order to train a classifier that is not affected by spurious correlation, we can partition training dataset into groups with multiple attributes \mathcal{A} based on some prior knowledge and then form the group using \mathcal{A} \times \mathcal{Y}. For example, the paper [1] observes that negation spuriously correlates with the contradiction label. Therefore, one natural choice of \mathcal{A} is “texts with negation words” and “texts without negation words;” this will lead to m=2 \times 3 = 6 groups.

• Improving Training on Data Mixture

  Training a classifier using a mixture of datasets \cup _ {k=1}^K \mathcal{D} _ k with the same label space \mathcal{Y}; this will give us K \times \vert \mathcal{Y}\vert groups. This is a more natural application of DRO as we have well-defined \mathcal{A} that does not depend on prior knowledge.

Method

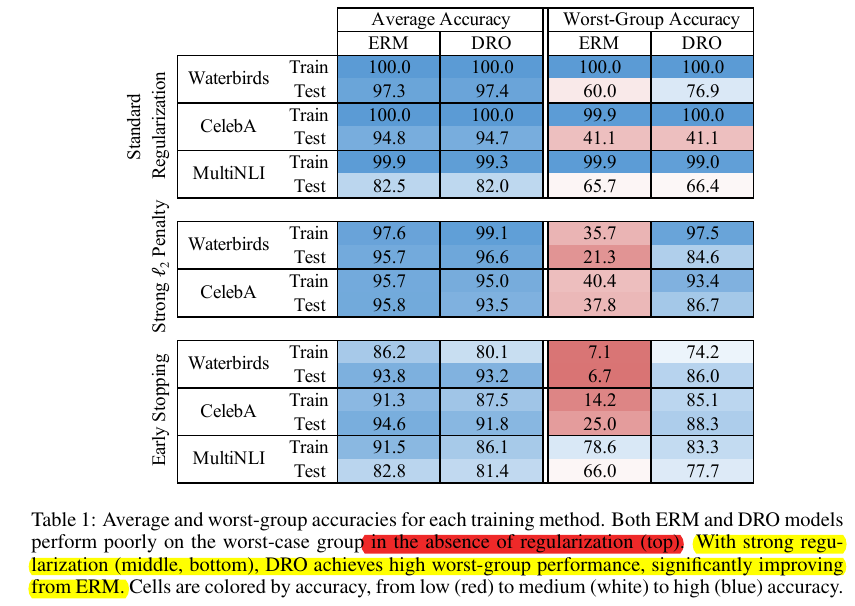
For large discriminative models, neither ERM nor gDRO is able to attain a low worst-group test error due to a high worst-group generalization gap.

Model	Method	Training Error	Worst-Group Test Error
Many Models	ERM	Low	High
Small Convex Discriminative Model or Generative Model	gDRO	Low	Low
Large Discriminative Model (e.g., ResNet or BERT)	gDRO	Low	High

The authors propose to add simple regularization to gDRO to address the problem; they try \ell_2 regularization and early stopping. Even though these methods are frequently used approaches, it is a novel complement to the observations in influential work [4]: regularization may be necessary to make gDRO work for large discriminative models.

Additional Note

• Probability Simplex

  A probability simplex \Delta is a geometric representation of all probabilities of n events. If there are n events, then \Delta is a (n-1)-dimensional convex set that includes all possible n-dimensional probability vectors \mathbf{p}; it satisfies \mathbf{1}^T \mathbf{p}=1 with non-negative entries. The boundary of \Delta is determined by extreme one-hot probability vectors.

  The visualization of a probability simplex depicting 3 events is a triangular plane determined by three extreme points (1, 0, 0), (0, 1, 0), (0,0, 1).

• Measures of Robustness

The paper uses the generalization on the worst-accuracy group as a proxy for robustness.

Reference

1. Right for the Wrong Reasons: Diagnosing Syntactic Heuristics in Natural Language Inference (McCoy et al., ACL 2019): This paper identifies three shortcuts (called “heuristics” in the paper) that could be exploited by an NLI classifier: (1) lexical overlap, (2) subsequence, and (3) constituent. The authors also propose the famous HANS (Heuristic Analysis for NLI Systems) test set to diagnose the shortcut learning.

   Instead of using these cases to overrule the lexical overlap heuristic, a model might account for them by learning to assume that the label is contradiction whenever there is negation in the premise but not the hypothesis.

2. Annotation Artifacts in Natural Language Inference Data (Gururangan et al., NAACL 2018): This paper shows that a significant portion of SNLI and MNLI test sets could be classified correctly without premises.
3. [1806.08010] Fairness Without Demographics in Repeated Loss Minimization (Hashimoto et al.): The application of DRO in fair classification.
4. [1611.03530] Understanding deep learning requires rethinking generalization (Zhang et al.; more than 5K citations): This paper makes two important observations and rules out the VC dimension, Rademacher complexity as possible explanations.
   • The neural network is able to attain zero training error for (1) a dataset with real images but random label, and (2) a dataset of random noise and random labels through memorization. The testing error is still near chance.
   • Because of the last bullet point, the regularization may not help with generalization at all; it is neither a necessary nor a sufficient condition to generalization.